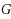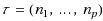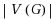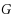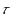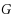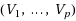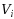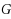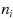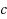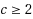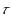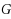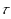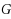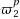Given a graph
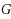 , a sequence
, a sequence
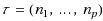 of positive integers summing up to
of positive integers summing up to
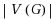 is said to be realizable in
is said to be realizable in
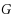 if there exists a realization of
if there exists a realization of
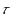 in
in
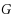 , i.e. a partition
, i.e. a partition
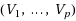 of
of
 such that each
such that each
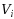 induces a connected subgraph of
induces a connected subgraph of
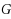 on
on
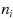 vertices. We first give a reduction showing that the problem of deciding whether a sequence with
vertices. We first give a reduction showing that the problem of deciding whether a sequence with
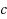 elements is realizable in a graph is NP‐complete for every fixed
elements is realizable in a graph is NP‐complete for every fixed
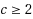 . Thanks to slight modifications of this reduction, we then prove additional hardness results on decision problems derived from the previous one. In particular, we show that the previous problem remains NP‐complete when a constant number of vertex‐membership constraints must be satisfied. We then prove the tightness of an easiness result proved independently by Györi and Lovász regarding a similar problem. We finally show that another graph partition problem, asking whether several partial realizations of
. Thanks to slight modifications of this reduction, we then prove additional hardness results on decision problems derived from the previous one. In particular, we show that the previous problem remains NP‐complete when a constant number of vertex‐membership constraints must be satisfied. We then prove the tightness of an easiness result proved independently by Györi and Lovász regarding a similar problem. We finally show that another graph partition problem, asking whether several partial realizations of
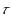 in
in
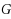 can be extended to obtain whole realizations of
can be extended to obtain whole realizations of
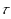 in
in
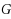 , is
, is
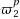 ‐complete.
‐complete.