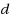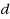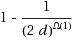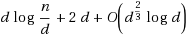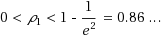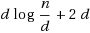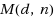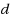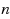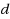A new randomized algorithm for group testing with unknown number of defective items

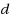In many fault detection problems, we want to identify defective items from a set of $n$ items using the minimum number of tests. Group testing is for the scenario where each test is on a subset of items, and tells whether the subset contains at least one defective item or not. In practice, the number $d$ of defective items is often unknown in advance. In this paper, we propose a new randomized group testing algorithm RPT (Randomized Parallel Testing) for the case where the number 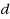$d$ of defective items is unknown in advance, such that with high probability 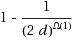$1‐\frac{1}{{\left(2d\right)}^{\mathrm{\Omega }\left(1\right)}}$ , the total number of tests performed by RPT is bounded from the above by 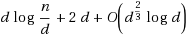$dlog\frac{n}{d}+2d+O(d^{\frac{2}{3}}logd)$ . 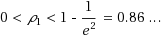If $0<d<{\mathit{\rho }}_{1}n$ for some constant $0<{\mathit{\rho }}_1<1‐\frac{1}{e^2}=0.86\dots$ , which holds for most practical applications, this upper bound is asymptotically smaller than previous best result. 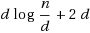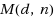In addition, we give a new upper bound $dlog\frac{n}{d}+2d$ on $M(d,n)$ , the minimum number of tests required in the worst case to identify all the 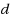$d$ defective items out of 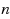$n$ items when the value of 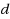$d$ is known in advance.