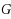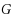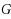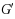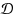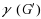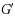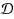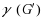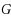| Article ID: | iaor201526110 |
| Volume: | 30 |
| Issue: | 1 |
| Start Page Number: | 109 |
| End Page Number: | 119 |
| Publication Date: | Jul 2015 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Sheikholeslami S, Karami H, Favaron O |
| Keywords: | combinatorial optimization, graphs |
The game domination subdivision number of a graph