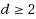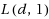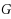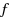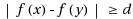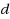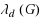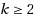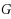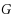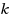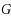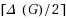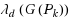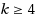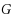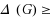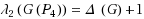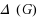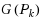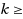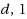For an integer
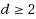 , an
, an
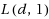 ‐labeling of a graph
‐labeling of a graph
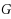 is a function
is a function
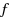 from its vertex set to the non‐negative integers such that
from its vertex set to the non‐negative integers such that
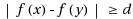 if vertices
if vertices
 and
and
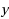 are adjacent, and
are adjacent, and
 1 if
1 if
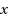 and
and
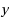 are at distance two. The minimum span over all the L(
are at distance two. The minimum span over all the L(
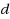 ,1)‐labelings of
,1)‐labelings of
 is denoted by
is denoted by
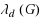 . For a given integer
. For a given integer
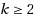 , the edge‐path‐replacement of
, the edge‐path‐replacement of
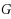 or
or
 is the graph obtained from
is the graph obtained from
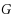 by replacing each edge with a path
by replacing each edge with a path
 on
on
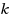 vertices. We show that the edges of
vertices. We show that the edges of
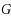 can be colored with
can be colored with
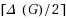 colors so that each monochromatic subgraph has maximum degree at most 2 and use this fact to establish general upper bounds on
colors so that each monochromatic subgraph has maximum degree at most 2 and use this fact to establish general upper bounds on
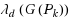 for
for
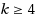 . As a corollary, we settle the following conjecture by Lü (J Comb Optim, 2012): for any graph
. As a corollary, we settle the following conjecture by Lü (J Comb Optim, 2012): for any graph
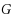 with
with
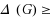 2,
2,
 + 2. Moreover,
+ 2. Moreover,
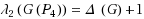 when
when
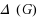 is even and different from 2. We also show that the class of graphs
is even and different from 2. We also show that the class of graphs
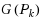 with
with
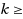 4 satisfies a conjecture by Havet and Yu (2008 Discrete Math 308:498–513) in the related area of (
4 satisfies a conjecture by Havet and Yu (2008 Discrete Math 308:498–513) in the related area of (
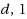 )‐total labeling of graphs.
)‐total labeling of graphs.