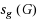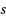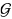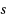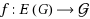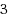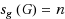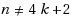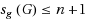| Article ID: | iaor201526103 |
| Volume: | 30 |
| Issue: | 1 |
| Start Page Number: | 1 |
| End Page Number: | 17 |
| Publication Date: | Jul 2015 |
| Journal: | Journal of Combinatorial Optimization |
| Authors: | Milani Martin, Anholcer Marcin, Cichacz Sylwia |
| Keywords: | graphs |
We investigate the