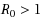Global dynamics of vector-borne diseases with horizontal transmission in host population

The paper presents the dynamical features of a vector–host epidemic model with direct transmission. First, we extended the model by taking into account the exposed individuals in both human and vector population with the impact of disease related deaths and total time dependent population size. Using Lyapunov function theory some sufficient conditions for global stability of both the disease‐free equilibrium and the endemic equilibrium are obtained. For the basic reproductive number $R_0>1$ , a unique endemic equilibrium exists and is globally asymptotically stable. Furthermore, it is found that the model exhibits the phenomenon of backward bifurcation, where the stable disease‐free equilibria coexists with a stable endemic equilibrium. Finally, numerical simulations are carried out to investigate the influence of the key parameters on the spread of the vector‐borne disease, to support the analytical conclusion and illustrate possible behavioral scenarios of the model.