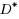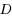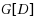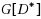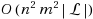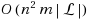An Incremental Polynomial Time Algorithm to Enumerate All Minimal Edge Dominating Sets

We show that all minimal edge dominating sets of a graph can be generated in incremental polynomial time. We present an algorithm that solves the equivalent problem of enumerating minimal (vertex) dominating sets of line graphs in incremental polynomial, and consequently output polynomial, time. Enumeration of minimal dominating sets in graphs has recently been shown to be equivalent to enumeration of minimal transversals in hypergraphs. The question whether the minimal transversals of a hypergraph can be enumerated in output polynomial time is a fundamental and challenging question; it has been open for several decades and has triggered extensive research. To obtain our result, we present a flipping method to generate all minimal dominating sets of a graph. Its basic idea is to apply a flipping operation to a minimal dominating set $D^{\ast }$ to generate minimal dominating sets $D$ such that $G[D]$ contains more edges than $G[D^{\ast }]$ . We show that the flipping method works efficiently on line graphs, resulting in an algorithm with delay $O(n^2{m}^2|\mathcal{L}|)$ between each pair of consecutively output minimal dominating sets, where $n$ and $m$ are the numbers of vertices and edges of the input graph, respectively, and $\mathcal{L}$ is the set of already generated minimal dominating sets. Furthermore, we are able to improve the delay to $O(n^{2}m|\mathcal{L}|)$ on line graphs of bipartite graphs. Finally we show that the flipping method is also efficient on graphs of large girth, resulting in an incremental polynomial time algorithm to enumerate the minimal dominating sets of graphs of girth at least 7.