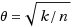Parameterized Algorithms for the 2-Clustering Problem with Minimum Sum and Minimum Sum of Squares Objective Functions

In the Min‐Sum 2‐Clustering problem, we are given a graph and a parameter k, and the goal is to determine if there exists a 2‐partition of the vertex set such that the total conflict number is at most k, where the conflict number of a vertex is the number of its non‐neighbors in the same cluster and neighbors in the different cluster. The problem is equivalent to 2‐Cluster Editing and 2‐Correlation Clustering with an additional multiplicative factor two in the cost function. In this paper we show an algorithm for Min‐Sum 2‐Clustering with time complexity O(n⋅2.619 ^r/(1−4r/n)+n ³), where n is the number of vertices and r=k/n. Particularly, the time complexity is O ^∗(2.619 ^k/n ) for k∈o(n ²) and polynomial for k∈O(nlogn), which implies that the problem can be solved in subexponential time for k∈o(n ²). We also design a parameterized algorithm for a variant in which the cost is the sum of the squared conflict‐numbers. 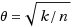For k∈o(n ³), the algorithm runs in subexponential O(n ³⋅5.171 ^θ ) time, where $\theta =\sqrt{k/n}$ .