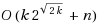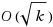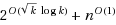| Article ID: | iaor201526358 |
| Volume: | 72 |
| Issue: | 3 |
| Start Page Number: | 778 |
| End Page Number: | 790 |
| Publication Date: | Jul 2015 |
| Journal: | Algorithmica |
| Authors: | Tamaki Hisao, Kobayashi Yasuaki |
| Keywords: | graphs, programming: dynamic, programming: linear |
We give a subexponential fixed parameter algorithm for one‐sided crossing minimization. It runs in