Max-Cut Parameterized Above the Edwards-Erdos Bound

We study the boundary of tractability for the Max‐Cut problem in graphs. Our main result shows that Max‐Cut parameterized above the Edwards‐Erdõs bound is fixed‐parameter tractable: we give an algorithm that for any connected graph with n vertices and m edges finds a cut of size 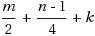$\frac{m}{2}+\frac{n‐1}{4}+k$ in time 2 ^O(k)⋅n ⁴, or decides that no such cut exists. This answers a long‐standing open question from parameterized complexity that has been posed a number of times over the past 15 years. Our algorithm has asymptotically optimal running time, under the Exponential Time Hypothesis, and is strengthened by a polynomial‐time computable kernel of polynomial size.