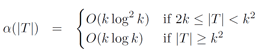An Improved Approximation Algorithm for the Minimum Cost Subset k-Connected Subgraph Problem

The minimum cost subset k‐connected subgraph problem is a cornerstone problem in the area of network design with vertex connectivity requirements. In this problem, we are given a graph G=(V,E) with costs on edges and a set of terminals T⊆V. The goal is to find a minimum cost subgraph such that every pair of terminals are connected by k openly (vertex) disjoint paths. In this paper, we present an approximation algorithm for the subset k‐connected subgraph problem which improves on the previous best approximation guarantee of O(k ²logk) by Nutov (ACM Trans. Algorithms 9(1):1, 2012). Our approximation guarantee, α(|T|), depends upon the number of terminals: 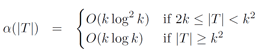$$\alpha (\mid T\mid )=\{\begin{array}{ll}O(k{\log }^{2}k)& \mathrm{if}2k\le \mid T\mid <k^2\\ O(k\log k)& \mathrm{if}\mid T\mid \ge k^2\end{array}$$ So, when the number of terminals is large enough, the approximation guarantee improves significantly. Moreover, we show that, given an approximation algorithm for |T|=k, we can obtain almost the same approximation guarantee for any instances with |T|> k. This suggests that the hardest instances of the problem are when |T|≈k.