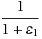Let ϵ
1,ϵ
2 be two non negative numbers. An approximate rectangle of influence drawing (also called (ϵ
1,ϵ
2)‐RID) is a proximity drawing of a graph such that: (i) if u,v are adjacent vertices then their rectangle of influence ‘scaled down’ by the factor
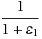 does not contain other vertices of the drawing; (ii) if u,v are not adjacent, then their rectangle of influence ‘blown‐up’ by the factor 1+ϵ
2 contains some vertices of the drawing other than u and v. Firstly, we prove that all planar graphs have an (ϵ
1,ϵ
2)‐RID for any ϵ
1>0 and ϵ
2>0, while there exist planar graphs which do not admit an (ϵ
1,0)‐RID and planar graphs which do not admit a (0,ϵ
2)‐RID. Then, we investigate (0,ϵ
2)‐RIDs; we prove that both the outerplanar graphs and a suitably defined family of graphs without separating 3‐cycles admit this type of drawing. Finally, we study polynomial area approximate rectangle of influence drawings and prove that (0,ϵ
2)‐RIDs of proper track planar graphs (a superclass of the outerplanar graphs) can be computed in polynomial area for any ϵ
2>2. As for values of ϵ
2 such that ϵ
2≤2, we describe a drawing algorithm that computes (0,ϵ
2)‐RIDs of binary trees in area
does not contain other vertices of the drawing; (ii) if u,v are not adjacent, then their rectangle of influence ‘blown‐up’ by the factor 1+ϵ
2 contains some vertices of the drawing other than u and v. Firstly, we prove that all planar graphs have an (ϵ
1,ϵ
2)‐RID for any ϵ
1>0 and ϵ
2>0, while there exist planar graphs which do not admit an (ϵ
1,0)‐RID and planar graphs which do not admit a (0,ϵ
2)‐RID. Then, we investigate (0,ϵ
2)‐RIDs; we prove that both the outerplanar graphs and a suitably defined family of graphs without separating 3‐cycles admit this type of drawing. Finally, we study polynomial area approximate rectangle of influence drawings and prove that (0,ϵ
2)‐RIDs of proper track planar graphs (a superclass of the outerplanar graphs) can be computed in polynomial area for any ϵ
2>2. As for values of ϵ
2 such that ϵ
2≤2, we describe a drawing algorithm that computes (0,ϵ
2)‐RIDs of binary trees in area
 , where c is a positive constant, f(ϵ
2) is a poly‐logarithmic function that tends to infinity as ϵ
2 tends to zero, and n is the number of vertices of the input tree.
, where c is a positive constant, f(ϵ
2) is a poly‐logarithmic function that tends to infinity as ϵ
2 tends to zero, and n is the number of vertices of the input tree.