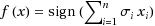A signed majority function is a linear threshold function f:{+1,−1}
n
→{+1,−1} of the form
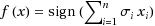 where each σ
i
∈{+1,−1}. Signed majority functions are a highly symmetrical subclass of the class of all linear threshold functions, which are functions of the form
where each σ
i
∈{+1,−1}. Signed majority functions are a highly symmetrical subclass of the class of all linear threshold functions, which are functions of the form
 for arbitrary real w
i
,θ. We study the query complexity of testing whether an unknown f:{+1,−1}
n
→{+1,−1} is a signed majority function versus ϵ-far from every signed majority function. While it is known (2010) that the broader class of all linear threshold functions is testable with poly(1/ϵ) queries (independent of n), prior to our work the best upper bound for signed majority functions was
for arbitrary real w
i
,θ. We study the query complexity of testing whether an unknown f:{+1,−1}
n
→{+1,−1} is a signed majority function versus ϵ-far from every signed majority function. While it is known (2010) that the broader class of all linear threshold functions is testable with poly(1/ϵ) queries (independent of n), prior to our work the best upper bound for signed majority functions was
 queries (via a non-adaptive algorithm), and the best lower bound was Ω(logn) queries for non-adaptive algorithms (2009). As our main results we exponentially improve both these prior bounds for testing signed majority functions:
(Upper bound) We give a poly(logn,1/ϵ)-query adaptive algorithm (which is computationally efficient) for this testing problem;
(Lower bound) We show that any non-adaptive algorithm for testing the class of signed majorities to constant accuracy must make n
Ω(1) queries. This directly implies a lower bound of Ω(logn) queries for any adaptive algorithm.
Our testing algorithm performs a sequence of restrictions together with consistency checks to ensure that each successive restriction is ‘compatible’ with the function prior to restriction. This approach is used to transform the original n-variable testing problem into a testing problem over poly(logn,1/ϵ) variables where a simple direct method can be applied. Analysis of the degree-1 Fourier coefficients plays an important role in our proofs.
queries (via a non-adaptive algorithm), and the best lower bound was Ω(logn) queries for non-adaptive algorithms (2009). As our main results we exponentially improve both these prior bounds for testing signed majority functions:
(Upper bound) We give a poly(logn,1/ϵ)-query adaptive algorithm (which is computationally efficient) for this testing problem;
(Lower bound) We show that any non-adaptive algorithm for testing the class of signed majorities to constant accuracy must make n
Ω(1) queries. This directly implies a lower bound of Ω(logn) queries for any adaptive algorithm.
Our testing algorithm performs a sequence of restrictions together with consistency checks to ensure that each successive restriction is ‘compatible’ with the function prior to restriction. This approach is used to transform the original n-variable testing problem into a testing problem over poly(logn,1/ϵ) variables where a simple direct method can be applied. Analysis of the degree-1 Fourier coefficients plays an important role in our proofs.