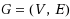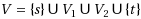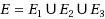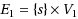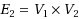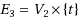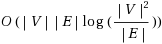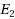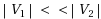Solving the parametric bipartite maximum flow problem in unbalanced and closure bipartite graphs

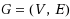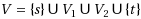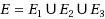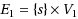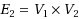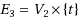Given a directed bipartite graph $G=(V,E)$ with a node set $V=\{s\}\cup V_1\cup V_2\cup \{t\}$ , and an arc set $E=E_1\cup E_2\cup E_3$ , where $E_1=\{s\}\times V_1$ , $E_2=V_1\times V_2$ , and $E_3=V_2\times \{t\}$ . Chen (1995) presented an 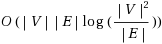$O(|V||E|log(\frac{{|V|}^2}{|E|}))$ time algorithm to solve the parametric bipartite maximum flow problem. In this paper, we assume all arcs in 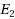$E_2$ have infinite capacity [such a graph is called closure graph Hochbaum (1998)], and present a new approach to solve the problem, which runs in $O(|V_1||E|log(\frac{|V_1{|}^2}{|E|}+2))$ time using Gallo et al’s parametric maximum flow algorithm, see Gallo et al. (1989). 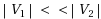In unbalanced bipartite graphs, we have $|V_1|<<|V_2|$ , so, our algorithm improves Chens’s algorithm in unbalanced and closure bipartite graphs.