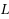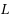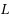On the L-approach for generating unconstrained two-dimensional non-guillotine cutting patterns

Many cutting problems on two- or three-dimensional objects require that the cuts be orthogonal and of guillotine type. However, there are applications in which the cuts must be orthogonal but need not be of guillotine type. In this paper we focus on the latter type of cuts on rectangular bins. We investigate the so-called $L$ -approach, introduced by Lins et al. (2003), which has been used to tackle, among others, the pallet loading problem and the two-dimensional unconstrained knapsack problem. This approach concerns a method to generate two $L$ -shaped pieces from an $L$ -shaped piece. More recently, Birgin et al. (2012), raised two questions concerning this approach. The first question is whether one may restrict only to cuts on raster points (rather than on all discretization points), without loss in the quality of the solution. We prove that the answer to this question is positive. The second question is whether the $L$ -approach is an optimal method to solve the unconstrained knapsack problem. We show an instance of the problem for which this approach fails to find an optimum solution.