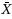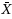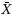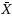Optimal designs of the double sampling &Xmacr; chart with estimated parameters

The double sampling (DS) 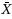$\overline{X}$ chart detects small and moderate mean shifts quickly. Furthermore, this chart can reduce the sample size. The DS 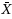$\overline{X}$ chart is usually investigated assuming that the process parameters are known. Nevertheless, the process parameters are usually unknown and are estimated from an in‐control Phase‐I dataset. This paper (i) evaluates the performances of the DS 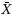$\overline{X}$ chart when process parameters are estimated by means of a new proposed theoretical method, (ii) shows that performances with estimated parameters are different from that with known parameters, and (iii) proposes three optimal design procedures: the first design minimizes the out‐of‐control average run length, the second design minimizes the in‐control average sample size and the third design minimizes the average extra quadratic loss, by considering the number of Phase‐I samples in these three designs. Additionally, for ease of implementation, this paper provides the new optimal parameters specially computed for the DS 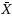$\overline{X}$ chart with estimated parameters, based on the number of Phase‐I samples used in practice. These findings will lead to a more economically feasible process monitoring situation, especially when the process parameters are unknown.