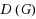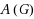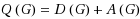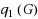| Article ID: | iaor2013905 |
| Volume: | 219 |
| Issue: | 10 |
| Start Page Number: | 5025 |
| End Page Number: | 5032 |
| Publication Date: | Jan 2013 |
| Journal: | Applied Mathematics and Computation |
| Authors: | Dilek (Gngr) Maden A, Das Kinkar Ch, Sinan evik A |
| Keywords: | combinatorial optimization, matrices |
Let