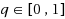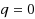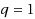Mixed SI (R) epidemic dynamics in random graphs with general degree distributions

Analytical description of disease propagation on random networks has become one of the most productive fields in recent years, yet more complex contact patterns and dynamics have been resorted to numerical study. In this paper, an epidemic model is defined in which each individual, once infected, has chances to recover from infection at certain rate. The chance is represented by a parameter $q\in [0\text{,}1]$ . This model can be viewed as an interpolation between classical SI model ( $q=0$ ) and SIR model ( $q=1$ ). We develop a low‐dimensional system of non‐linear ordinary differential equations to model the mixed susceptible‐infected (‐recovered) SI (R) epidemics on random network with general degree distributions. Both the final size of epidemics and the time‐dependent behaviors are derived within this simple framework. In addition, we present the exact transmissibility and the epidemic threshold for this model.