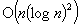Local minima for indefinite Quadratic Knapsack Problems

The paper considers the complexity of finding a local minimum for the nonconvex Quadratic Knapsack Problem. Global minimization for this example of quadratic programming is NP-hard. Moré and Vavasis have investigated the compelxity of local minimization for the strictly concave case of QKP; here their algorithm has been extended to the general indefinite case. The main result is an algorithm that computes a local minimum in steps. The present approach involves eliminating all but one of the convex variables through parametrization, yielding a nondifferentiable problem. A technique from computational geometry is used to address the nondifferentiable problem.