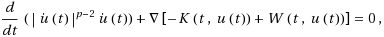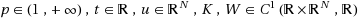| Article ID: | iaor20122100 |
| Volume: | 218 |
| Issue: | 13 |
| Start Page Number: | 7164 |
| End Page Number: | 7173 |
| Publication Date: | Mar 2012 |
| Journal: | Applied Mathematics and Computation |
| Authors: | Zhang Qiongfen, Tang X H |
| Keywords: | sets, programming: linear |
By applying a variant version of Mountain Pass Theorem in critical point theory, the existence of homoclinic solutions is obtained for the following asymptotically