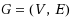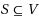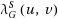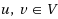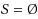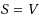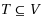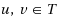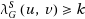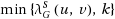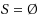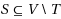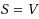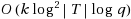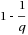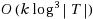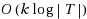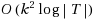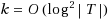A note on labeling schemes for graph connectivity

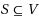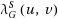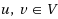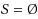Let $G=(V,E)$ be an undirected graph and let $S\subseteq V$ . The S‐connectivity ${\lambda }_G^S(u,v)$ of $u,v\in V$ is the maximum number of uv‐paths that no two of them have an edge or a node in $S\backslash \{u,v\}$ in common. Edge‐connectivity is the case $S=Ø$ and node‐connectivity is the case 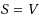$S=V$ . Given an integer k and a subset 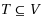$T\subseteq V$ of terminals, we consider the problem of assigning small ‘labels’ (binary strings) to the terminals, such that given the labels of two terminals 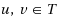$u,v\in T$ , one can decide whether 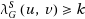${\lambda }_G^S(u,v)⩾k$ (k‐partial labeling scheme) or to return 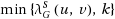$\min \{{\lambda }_G^S(u,v),k\}$ (k‐full labeling scheme). We observe that the best known labeling schemes for edge‐connectivity (the case 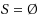$S=Ø$ ) extend to element‐connectivity (the case 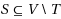$S\subseteq V\backslash T$ ), and use it to obtain a simple k‐full labeling scheme for node‐connectivity (the case 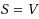$S=V$ ). If q distinct queries are expected, our k‐full scheme has max‐label size 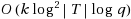$O(k{\log }^2|T|\log q)$ , with success probability 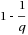$1‐\frac{1}{q}$ for all queries. We also give a deterministic k‐full labeling scheme with max‐label size 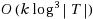$O(k{\log }^3|T|)$ . Recently, Hsu and Lu (2009) gave an optimal 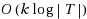$O(k\log |T|)$ labeling scheme for the k‐partial case. This implies an 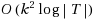$O(k^2\log |T|)$ labeling scheme for the k‐full case. 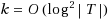Our deterministic k‐full labeling scheme is better for $k=O({\log }^2|T|)$ .