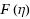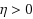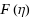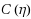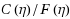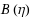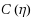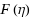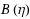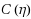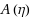We extended the method of McDougall and Stoner (1938) [15] to the computation of a general integral of the Fermi–Dirac distribution,
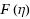 . When
. When
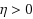 , the new method splits
, the new method splits
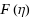 into a sum of three parts,
into a sum of three parts,
 , and
, and
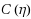 , and integrates them exactly and/or numerically by means of the double‐exponential quadrature rules. As η increases,
, and integrates them exactly and/or numerically by means of the double‐exponential quadrature rules. As η increases,
 damps algebraically while
damps algebraically while
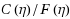 decays exponentially. Thus, they can be ignored when η exceeds certain threshold values depending on the input error tolerance. When
decays exponentially. Thus, they can be ignored when η exceeds certain threshold values depending on the input error tolerance. When
 is exactly computable and η is sufficiently large such that
is exactly computable and η is sufficiently large such that
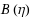 and
and
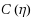 are negligible, the new method was 60–1000 times faster than the numerical integration of
are negligible, the new method was 60–1000 times faster than the numerical integration of
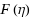 . Even if
. Even if
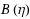 and/or
and/or
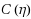 are not negligible, their smallness and rapid decay significantly accelerate their numerical quadrature so that the speed‐up factor becomes 3–20 unless η is less than 2.0–4.5. On the other hand, when
are not negligible, their smallness and rapid decay significantly accelerate their numerical quadrature so that the speed‐up factor becomes 3–20 unless η is less than 2.0–4.5. On the other hand, when
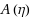 is numerically integrated, the speed‐up factor diminishes to 2–5. Still, the superiority of the new method to the numerical integration of
is numerically integrated, the speed‐up factor diminishes to 2–5. Still, the superiority of the new method to the numerical integration of
 is unchanged.
is unchanged.