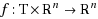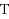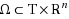| Article ID: | iaor20142056 |
| Volume: | 238 |
| Start Page Number: | 289 |
| End Page Number: | 299 |
| Publication Date: | Jul 2014 |
| Journal: | Applied Mathematics and Computation |
| Authors: | Diblk Josef, Vtovec Jir |
| Keywords: | programming: nonlinear, programming: dynamic, differential equations |
In this paper we study the asymptotic behavior of solutions of nonlinear dynamic systems on time scales of the form