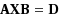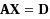Determinantal representations of the Drazin inverse over the quaternion skew field with applications to some matrix equations

Within the framework of the theory of the column and row determinants, we obtain determinantal representations of the Drazin inverse both for Hermitian and arbitrary matrices over the quaternion skew field. Using the obtained determinantal representations of the Drazin inverse we get explicit representation formulas (analogs of Cramer’s rule) for the Drazin inverse solutions of a quaternion matrix equation $\mathbf{AXB}=\mathbf{D}$ and consequently $\mathbf{AX}=\mathbf{D}$ , and $\mathbf{XB}=\mathbf{D}$ in two cases if $\mathbf{A}\text{,}\mathbf{B}$ are Hermitian or arbitrary.