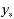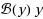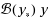| Article ID: | iaor20141993 |
| Volume: | 271 |
| Start Page Number: | 307 |
| End Page Number: | 318 |
| Publication Date: | Dec 2014 |
| Journal: | Journal of Computational and Applied Mathematics |
| Authors: | Einkemmer Lukas, Ostermann Alexander |
| Keywords: | simulation, numerical analysis |
In this paper we consider splitting methods for nonlinear ordinary differential equations in which one of the (partial) flows that results from the splitting procedure cannot be computed exactly. Instead, we insert a well‐chosen state