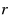Functionally-fitted block methods for ordinary differential equations

Functionally‐fitted methods generalize collocation techniques to integrate exactly a chosen set of linearly independent functions. In this paper, we propose a new type of functionally‐fitted block methods for ordinary differential equations. The basic theory for the proposed methods is established. First, we derive two sufficient conditions to ensure the existence of the functionally‐fitted block methods, discuss their equivalence to collocation methods in a special case and independence on integration time for a set of separable basis functions. We then obtain some basic characteristics of the methods by Taylor series expansions, and show that the order of accuracy of the $r$ ‐point functionally‐fitted block method is at least $r$ for general ordinary differential equations. Experimental results are conducted to demonstrate the validity of the functionally‐fitted block methods.