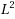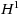A modified weak Galerkin finite element method for a class of parabolic problems

In this paper, we consider the solution of parabolic equation using the modified weak Galerkin finite element procedure, which is named as MWG‐FEM, based on the conception of the modified weak derivative over discontinuous functions with heterogeneous properties, in which the classical gradient operator is replaced by a modified weak gradient operator. Optimal order error estimates in a discrete $L^2$ norm and $H^1$ norm are established for the corresponding modified weak Galerkin finite element solutions. Finally, we numerically verify the convergence theory for the MWG‐FEM through some examples.