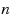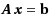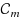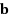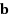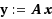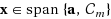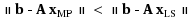| Article ID: | iaor20141813 |
| Volume: | 67 |
| Issue: | 10 |
| Start Page Number: | 1998 |
| End Page Number: | 2014 |
| Publication Date: | Jun 2014 |
| Journal: | Computers and Mathematics with Applications |
| Authors: | Liu Chein-Shan |
| Keywords: | heuristics |
A better method than the least squares solution is proposed in this paper to solve an