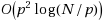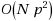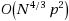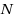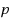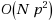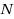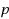In this paper we present computational cost estimates for parallel shared memory isogeometric multi‐frontal solvers. The estimates show that the ideal isogeometric shared memory parallel direct solver scales as
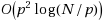 for one dimensional problems,
for one dimensional problems,
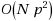 for two dimensional problems, and
for two dimensional problems, and
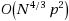 for three dimensional problems, where
for three dimensional problems, where
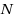 is the number of degrees of freedom, and
is the number of degrees of freedom, and
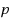 is the polynomial order of approximation. The computational costs of the shared memory parallel isogeometric direct solver are compared with those corresponding to the sequential isogeometric direct solver, being the latest equal to
is the polynomial order of approximation. The computational costs of the shared memory parallel isogeometric direct solver are compared with those corresponding to the sequential isogeometric direct solver, being the latest equal to
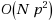 for the one dimensional case,
for the one dimensional case,
 for the two dimensional case, and
for the two dimensional case, and
 for the three dimensional case. The shared memory version significantly reduces both the scalability in terms of
for the three dimensional case. The shared memory version significantly reduces both the scalability in terms of
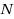 and
and
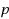 . Theoretical estimates are compared with numerical experiments performed with linear, quadratic, cubic, quartic, and quintic B‐splines, in one and two spatial dimensions.
. Theoretical estimates are compared with numerical experiments performed with linear, quadratic, cubic, quartic, and quintic B‐splines, in one and two spatial dimensions.