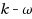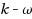On numerical simulation of three-dimensional flow problems by finite element and finite volume techniques

This paper is interested in the numerical approximation of the turbulent 3D incompressible flow. The turbulent flow is mathematically modeled using the Reynolds averaged Navier–Stokes (RANS) equations and two classes of the turbulent models are considered. RANS equations are approximated by two numerical techniques, the finite volume and the finite element methods. The finite element approximation on general 3D domains using general meshes consisting of hexahedrons as well as tetrahedrons, pyramids and prisms is described. The definition of the continuous piecewise trilinear/linear finite element space is given, and the stabilization based on the streamline‐upwind/Petrov–Galerkin method together with the pressure stabilizing/Petrov–Galerkin techniques is used. The turbulence $k\text{–}\omega$ model is approximated on the finite element spaces, and the nonlinear stabilization technique is applied. Furthermore, the finite volume technique is used for the approximation of the RANS equations. The turbulent $k\text{–}\omega$ or the explicit algebraic Reynolds stress models are used. The numerical solution is carried out by the implicit finite volume method. The artificial compressibility method is used to solve the incompressibility constraint. The numerical results are shown.