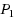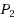Indeterminate constants in numerical approximations of PDEs: A pilot study using data mining techniques

Rolle’s theorem, and therefore, Lagrange and Taylor’s theorems are responsible for the inability to determine precisely the error estimate of numerical methods applied to partial differential equations. Basically, this comes from the existence of a non unique unknown point which appears in the remainder of Taylor’s expansion. In this paper we consider the case of finite elements method. We show in detail how Taylor’s theorem gives rise to indeterminate constants in the a priori error estimates. As a consequence, we highlight that classical conclusions have to be reformulated if one considers local error estimate. To illustrate our purpose, we consider the implementation of $P_1$ and $P_2$ finite elements method to solve Vlasov–Maxwell equations in a paraxial configuration. If the Bramble–Hilbert theorem claims that global error estimates for finite elements $P_2$ are ‘better’ than the $P_1$ ones, we show how data mining techniques are powerful to identify and to qualify when and where local numerical results of $P_1$ and $P_2$ are equivalent.