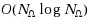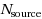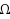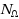A fast solver for Poisson problems on infinite regular lattices

The Fast Multipole Method (FMM) provides a highly efficient computational tool for solving constant coefficient partial differential equations (e.g. the Poisson equation) on infinite domains. The solution to such an equation is given as the convolution between a fundamental solution and the given data function, and the FMM is used to rapidly evaluate the sum resulting upon discretization of the integral. This paper describes an analogous procedure for rapidly solving elliptic difference equations on infinite lattices. In particular, a fast summation technique for a discrete equivalent of the continuum fundamental solution is constructed. The asymptotic complexity of the proposed method is $O\left(N_{\mathrm{source}}\right)$ , where $N_{\mathrm{source}}$ is the number of points subject to body loads. This is in contrast to FFT based methods which solve a lattice Poisson problem at a cost $O(N_{\Omega }log{N}_{\Omega })$ independent of $N_{\mathrm{source}}$ , where $\Omega$ is an artificial rectangular box containing the loaded points and $N_{\Omega }$ is the number of lattice points in $\Omega$ .