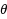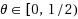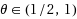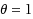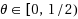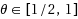Choice of θ and mean-square exponential stability in the stochastic theta method of stochastic differential equations

This paper examines the relationship of choice of 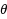$\theta$ and mean‐square exponential stability in the stochastic theta method (STM) of stochastic differential equations (SDEs) and mainly includes the following three results: (i) under the linear growth condition for the drift term, when 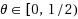$\theta \in [0,1/2)$ , the STM may preserve the mean‐square exponential stability of the exact solution, but the counterexample shows that the STM cannot reproduce this stability without this linear growth condition; (ii) when 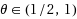$\theta \in (1/2,1)$ , without the linear growth condition for the drift term, the STM may reproduce the mean‐square exponential stability of the exact solution, but the bound of the Lyapunov exponent cannot be preserved; (iii) when 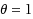$\theta =1$ (this STM is called as the backward Euler–Maruyama (BEM) method), the STM can reproduce not only the mean‐square exponential stability, but also the bound of the Lyapunov exponent. 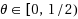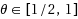This paper also gives the sufficient and necessary conditions of the mean‐square exponential stability of the STM for the linear SDE when $\theta \in [0,1/2)$ and $\theta \in [1/2,1]$ , respectively, and the simulations also illustrate these theoretical results.