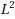Convergence and quasi-optimality of adaptive FEM with inhomogeneous Dirichlet data

We consider the solution of a second order elliptic PDE with inhomogeneous Dirichlet data by means of adaptive lowest‐order FEM. As is usually done in practice, the given Dirichlet data are discretized by nodal interpolation. As model example serves the Poisson equation with mixed Dirichlet–Neumann boundary conditions. For error estimation, we use an edge‐based residual error estimator which replaces the volume residual contributions by edge oscillations. For 2D, we prove convergence of the adaptive algorithm even with optimal convergence rate. For 2D and 3D, we show convergence if the nodal interpolation operator is replaced by the $L^2$ ‐projection or the Scott–Zhang quasi‐interpolation operator. As a byproduct of the proof, we show that the Scott–Zhang operator converges pointwise to a limiting operator as the mesh is locally refined. This property might be of independent interest besides the current application. Finally, numerical experiments conclude the work.