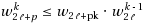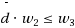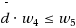We investigate the growth of the number w
k
of walks of length k in undirected graphs as well as related inequalities. In the first part, we deduce the inequality w
2a+c
⋅w
2(a+b)+c
≤w
2a
⋅w
2(a+b+c), which we call the Sandwich Theorem. It unifies and generalizes an inequality by Lagarias et al. and an inequality by Dress and Gutman. In the same way, we derive the inequality w
2a+c
(v,v)⋅w
2(a+b)+c
(v,v)≤w
2a
(v,v)⋅w
2(a+b+c)(v,v) for the number w
k
(v,v) of closed walks of length k starting at a given vertex v. We then use a theorem of Blakley and Dixon to show
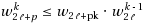 , which unifies and generalizes an inequality by Erdõs and Simonovits and, again, the inequality by Dress and Gutman. Both results can be translated directly into the corresponding forms using the higher order densities, which extends former results. In the second part, we provide a new family of lower bounds for the largest eigenvalue λ
1 of the adjacency matrix based on closed walks. We apply the Sandwich Theorem to show monotonicity in this and a related family of lower bounds of Nikiforov. This leads to generalized upper bounds for the energy of graphs. In the third part, we demonstrate that a further natural generalization of the Sandwich Theorem is not valid for general graphs. We show that the inequality w
a+b
⋅w
a+b+c
≤w
a
⋅w
a+2b+c
does not hold even in very restricted cases like w
1⋅w
2≤w
0⋅w
3 (i.e.,
, which unifies and generalizes an inequality by Erdõs and Simonovits and, again, the inequality by Dress and Gutman. Both results can be translated directly into the corresponding forms using the higher order densities, which extends former results. In the second part, we provide a new family of lower bounds for the largest eigenvalue λ
1 of the adjacency matrix based on closed walks. We apply the Sandwich Theorem to show monotonicity in this and a related family of lower bounds of Nikiforov. This leads to generalized upper bounds for the energy of graphs. In the third part, we demonstrate that a further natural generalization of the Sandwich Theorem is not valid for general graphs. We show that the inequality w
a+b
⋅w
a+b+c
≤w
a
⋅w
a+2b+c
does not hold even in very restricted cases like w
1⋅w
2≤w
0⋅w
3 (i.e.,
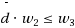 ) in the context of bipartite or cycle free graphs. In contrast, we show that surprisingly this inequality is always satisfied for trees and we show how to construct worst‐case instances (regarding the difference of both sides of the inequality) for a given degree sequence. We also prove the inequality w
1⋅w
4≤w
0⋅w
5 (i.e.,
) in the context of bipartite or cycle free graphs. In contrast, we show that surprisingly this inequality is always satisfied for trees and we show how to construct worst‐case instances (regarding the difference of both sides of the inequality) for a given degree sequence. We also prove the inequality w
1⋅w
4≤w
0⋅w
5 (i.e.,
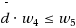 ) for trees and conclude with a corresponding conjecture for longer walks.
) for trees and conclude with a corresponding conjecture for longer walks.