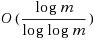Efficient Coordination Mechanisms for Unrelated Machine Scheduling

We present three new coordination mechanisms for scheduling n selfish jobs on m unrelated machines. A coordination mechanism aims to mitigate the impact of selfishness of jobs on the efficiency of schedules by defining a local scheduling policy on each machine. The scheduling policies induce a game among the jobs and each job prefers to be scheduled on a machine so that its completion time is minimum given the assignments of the other jobs. We consider the maximum completion time among all jobs as the measure of the efficiency of schedules. The approximation ratio of a coordination mechanism quantifies the efficiency of pure Nash equilibria (price of anarchy) of the induced game. Our mechanisms are deterministic, local, and preemptive in the sense that the scheduling policy does not necessarily process the jobs in an uninterrupted way and may introduce some idle time. Our first coordination mechanism has approximation ratio Θ(logm) and always guarantees that the induced game has pure Nash equilibria to which the system converges in at most n rounds. This result improves a bound of O(log² m) due to Azar, Jain, and Mirrokni and, similarly to their mechanism, our mechanism uses a global ordering of the jobs according to their distinct IDs. Next we study the intriguing scenario where jobs are anonymous, i.e., they have no IDs. In this case, coordination mechanisms can only distinguish between jobs that have different load characteristics. Our second mechanism handles anonymous jobs and has approximation ratio 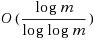$O(\frac{\log m}{\log \log m})$ although the game induced is not a potential game and, hence, the existence of pure Nash equilibria is not guaranteed by potential function arguments. However, it provides evidence that the known lower bounds for non‐preemptive coordination mechanisms could be beaten using preemptive scheduling policies. Our third coordination mechanism also handles anonymous jobs and has a nice ‘cost‐revealing’ potential function. We use this potential function in order, not only to prove the existence of equilibria, but also to upper‐bound the price of stability of the induced game by O(logm) and the price of anarchy by O(log² m). Our third coordination mechanism is the first that handles anonymous jobs and simultaneously guarantees that the induced game is a potential game and has bounded price of anarchy. In order to obtain the above bounds, our coordination mechanisms use m as a parameter. Slight variations of these mechanisms in which this information is not necessary achieve approximation ratios of O(m ^ϵ ), for any constant ϵ>0.