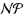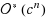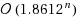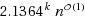| Article ID: | iaor2013300 |
| Volume: | 65 |
| Issue: | 1 |
| Start Page Number: | 95 |
| End Page Number: | 128 |
| Publication Date: | Jan 2013 |
| Journal: | Algorithmica |
| Authors: | Liedloff Mathieu, Fernau Henning, Binkele-Raible Daniel, Gaspers Serge |
| Keywords: | combinatorial optimization |
We consider the