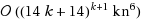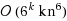The NP‐complete problem Proper Interval Vertex Deletion is to decide whether an input graph on n vertices and m edges can be turned into a proper interval graph by deleting at most k vertices. Van Bevern et al. (In: Proceedings WG 2010. Lecture notes in computer science, vol. 6410, pp. 232–243, 2010) showed that this problem can be solved in
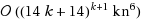 time. We improve this result by presenting an
time. We improve this result by presenting an
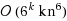 time algorithm for Proper Interval Vertex Deletion. Our fixed‐parameter algorithm is based on a new structural result stating that every connected component of a {claw,net,tent,C
4,C
5,C
6}‐free graph is a proper circular arc graph, combined with a simple greedy algorithm that solves Proper Interval Vertex Deletion on {claw,net,tent,C
4,C
5,C
6}‐free graphs in
time algorithm for Proper Interval Vertex Deletion. Our fixed‐parameter algorithm is based on a new structural result stating that every connected component of a {claw,net,tent,C
4,C
5,C
6}‐free graph is a proper circular arc graph, combined with a simple greedy algorithm that solves Proper Interval Vertex Deletion on {claw,net,tent,C
4,C
5,C
6}‐free graphs in
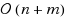 time. Our approach also yields a polynomial‐time 6‐approximation algorithm for the optimization variant of Proper Interval Vertex Deletion.
time. Our approach also yields a polynomial‐time 6‐approximation algorithm for the optimization variant of Proper Interval Vertex Deletion.