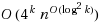Computing Optimal Steiner Trees in Polynomial Space

Given an n‐node edge‐weighted graph and a subset of k terminal nodes, the NP‐hard (weighted) Steiner tree problem is to compute a minimum‐weight tree which spans the terminals. All the known algorithms for this problem which improve on trivial O(1.62 ⁿ )‐time enumeration are based on dynamic programming, and require exponential space. Motivated by the fact that exponential‐space algorithms are typically impractical, in this paper we address the problem of designing faster polynomial‐space algorithms. Our first contribution is a simple O((27/4) ^k n ^O(logk))‐time polynomial‐space algorithm for the problem. This algorithm is based on a variant of the classical tree‐separator theorem: every Steiner tree has a node whose removal partitions the tree in two forests, containing at most 2k/3 terminals each. Exploiting separators of logarithmic size which evenly partition the terminals, we are able to reduce the running time to 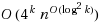$O(4^k{n}^{O({\log }^{2}k)})$ . This improves on trivial enumeration for roughly k <n/3, which covers most of the cases of practical interest. Combining the latter algorithm (for small k) with trivial enumeration (for large k) we obtain a O(1.59 ⁿ )‐time polynomial‐space algorithm for the weighted Steiner tree problem. As a second contribution of this paper, we present a O(1.55 ⁿ )‐time polynomial‐space algorithm for the cardinality version of the problem, where all edge weights are one. This result is based on a improved branching strategy. The refined branching is based on a charging mechanism which shows that, for large values of k, convenient local configurations of terminals and non‐terminals exist. The analysis of the algorithm relies on the Measure & Conquer approach: the non‐standard measure used here is a linear combination of the number of nodes and number of non‐terminals. Using a recent result in Nederlof (International colloquium on automata, languages and programming (ICALP), pp. 713–725, 2009), the running time can be reduced to O(1.36 ⁿ ). The previous best algorithm for the cardinality case runs in O(1.42 ⁿ ) time and exponential space.