Computing a Hamiltonian Path of Minimum Euclidean Length Inside a Simple Polygon

Given an n‐vertex convex polygon, we show that a shortest Hamiltonian path visiting all vertices without imposing any restriction on the starting and ending vertices of the path can be found in O(nlogn) time and Θ(n) space. The time complexity increases to O(nlog² n) for computing this path inside an n‐vertex simple polygon. The previous best algorithms for these problems are quadratic in time and space. For our purposes, we reformulate the above shortest‐path problems in terms of a dynamic programming scheme involving falling staircase anti‐Monge weight‐arrays, and, in addition, we provide an O(nlogn) time and Θ(n) space algorithm to solve the following one‐dimensional dynamic programming recurrence 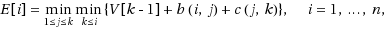$E[i]=\underset{1\le j\le k}{\min }\underset{k\le i}{\min }\{V[k‐1]+b(i,j)+c(j,k)\},i=1,\dots ,n,$ where V[0] is known, V[k], for k=1,…,n, can be computed from E[k] in constant time, and B={b(i,j)} and C={c(j,k)} are known falling staircase anti‐Monge weight‐arrays of size n×n.