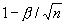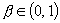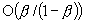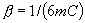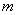On the convergence of the affine-scaling algorithm

The affine-scaling algorithm, first proposed by Dikin, is presently enjoying great popularity as a potentially effective means of solving linear programs. An outstanding question about this algorithm concerns its convergence in the presence of degeneracy. In this paper, the authors give new convergence results for this algorithm that do not require any non-degeneracy assumption on the problem. In particular, they show that if the stepsize choice of either Dikin or Barnes or Vanderbei, et al. is used, then the algorithm generates iterates that converge at least linearly with a convergence ratio of , where n is the number of variables and is a certain stepsize ratio. For one particular stepsize choice which is an extension of that of Barnes, the authors show that the cost of the limit point is within of the optimal cost and, for β sufficiently small (roughly, proportional to how close the cost of the nonoptimal vertices are to the optimal cost), is exactly optimal. They prove the latter result by using an unusual proof technique, that of analyzing the ergodic convergence of the corresponding dual vectors. For the special case of network flow problems with integer data, the authors show that it suffices to take , where is the number of constraints and is the sum of the cost coefficients, to attain exact optimality.