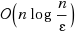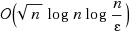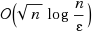An interior-point algorithm for linear optimization based on a new barrier function

Primal–dual interior‐point methods (IPMs) are the most efficient methods for a computational point of view. At present the theoretical iteration bound for small‐update IPMs is better than the one for large‐update IPMs. However, in practice, large‐update IPMs are much more efficient than small‐update IPMs. Peng et al. proposed new variants of IPMs based on self‐regular barrier functions and proved so far the best known complexity, e.g. $\mathcal{O}\left(\sqrt{n}\log n\log \frac{n}{ϵ}\right)$ , for large‐update IPMs with some specific self‐regular barrier functions. Recently, Roos et al. proposed new primal–dual IPMs based on various barrier functions to improve the iteration bound for large‐update methods from $\mathcal{O}\left(n\log \frac{n}{ϵ}\right)$ to $\mathcal{O}\left(\sqrt{n}\log n\log \frac{n}{ϵ}\right)$ . Motivated by their works we define a new barrier function and propose a new primal–dual interior point algorithm based on this function for linear optimization (LO) problems. We show that the new algorithm has $\mathcal{O}\left(\sqrt{n}\log n\log \frac{n}{ϵ}\right)$ iteration bound for large‐update and $\mathcal{O}\left(\sqrt{n}\log \frac{n}{ϵ}\right)$ for small‐update methods which are currently the best known bounds, respectively.