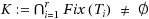Convergence of hybrid steepest descent method for variational inequalities in Banach spaces

Let E be a q‐uniformly smooth real Banach space with constant d q , q >1. Let T i : E → E, i =1,2,…, r be a finite family of nonexpansive mappings with 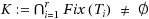$K≔{\cap }_{i=1}^r\mathit{Fix}(T_i)\ne \varnothing$ and K = Fix(T r T r‐1 … T 1)= Fix(T 1 T r … T 2)=···= Fix(T r‐1 T r‐2 … T r ). Let G : E → E be an η‐strongly accretive map which is also κ‐Lipschitzian. A hybrid steepest descent method introduced by Yamada and studied by various authors is proved to converge strongly to the unique solution of the variational inequality problem VI(G, K) in q‐uniformly smooth real Banach space, in particular, in L p spaces 1< p <∞.