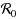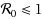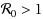Global stability of delay multigroup epidemic models with group mixing and nonlinear incidence rates

In this paper, we present a new delay multigroup SEIR model with group mixing and nonlinear incidence rates and investigate its global stability. We establish that the global dynamics of the models are completely determined by the basic reproduction number ${\mathcal{R}}_0$ . It is shown that, if ${\mathcal{R}}_0⩽1$ , then the disease free equilibrium is globally asymptotically stable and the disease dies out; if ${\mathcal{R}}_0>1$ , there exists a unique endemic equilibrium that is globally asymptotically stable and thus the disease persists in the population. Finally, a numerical example is also discussed to illustrate the effectiveness of the results.