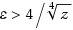We consider the problem of doing fast and reliable estimation of the number z of non‐zero entries in a sparse boolean matrix product. This problem has applications in databases and computer algebra. Let n denote the total number of non‐zero entries in the input matrices. We show how to compute a 1±ϵ approximation of z (with small probability of error) in expected time for any
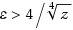. The previously best estimation algorithm, due to Cohen (J. Comput. Syst. Sci. 53(3):441–453, 1997), uses time . We also present a variant using I/Os in expectation in the cache‐oblivious model. In contrast to these results, the currently best algorithms for computing a sparse boolean matrix product use time ω(n
4/3) (resp. ω(n
4/3/B) I/Os), even if the result matrix is restricted to nonzero entries. Our algorithm combines the size estimation technique of Bar‐Yossef et al. (Proceedings of the 6th International Workshop on Randomization and Approximation Techniques (RANDOM ‘02), pp. 1–10, 2002) with a particular class of pairwise independent hash functions that allows the sketch of a set of the form to be computed in expected time and I/Os. We then describe how sampling can be used to maintain (independent) sketches of matrices that allow estimation to be performed in time o(n) if z is sufficiently large. This gives a simpler alternative to the sketching technique of Ganguly et al. (Proceedings of the 24th ACM Symposium on Principles of Database Systems (PODS ‘05), pp. 259–270, 2005), and matches a space lower bound shown in that paper. Finally, we present experiments on real‐world data sets that show the accuracy of both our methods to be significantly better than the worst‐case analysis predicts.
