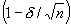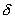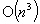A path following algorithm for a class of convex programming problems

The paper presents a primal-dual path following interior algorithm for a class of linearly constrained convex programming problems with non-negative decision variables. It introduces the definition of a Scaled Lipschitz Condition and shows that if the objective function satisfies the Scaled Lipschitz Condition then, at each iteration, the present algorithm reduces the duality gap by at least a factor of , where is positive and depends on the curvature of the objective function, by means of solving a system of linear equations which requires no more than arithmetic operations. The class of functions having the Scaled Lipschitz Condition includes linear, convex quadratic and entropy functions.