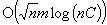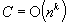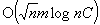New scaling algorithms for the assignment and minimum mean cycle problems

In this paper the authors suggest new scaling algorithms for the assignment and minimum mean cycle problems. The present assignment algorithm is based on applying scaling to a hybrid version of the recent auction algorithm of Bertsekas and the successive shortest path algorithm. The algorithm proceeds by relaxing the optimality conditions, and the amount of relaxation is successively reduced to zero. On a network with 2n nodes, m arcs, and integer arc costs bounded by C, the algorithm runs in time and uses very simple data structures. This time bound is comparable to the time taken by Gabow and Tarjan's scaling algorithm, and is better than all other time bounds under the similarity assumption, i.e., for some k. The authors consider the minimum mean cycle problem. The mean cost of a cycle is defined as the cost of the cycle divided by the number of arcs it contains. The minimum mean cycle problem is to identify a cycle whose mean cost is minimum. The authors show that by using ideas of the assignment algorithm in an approximate binary search procedure, the minimum mean cycle problem can also be solved in time. Under the similarity assumption, this is the best available time bound to solve the minimum mean cycle problem.