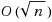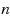Batch scheduling of identical jobs with controllable processing times

In scheduling models with controllable processing times, the job processing times can be controlled (i.e. compressed) by allocating additional resources. In batch scheduling a large number of jobs may be grouped and processed as separate batches, where a batch processing time is identical to the total processing times of the jobs contained in the batch, and a setup time is incurred when starting a new batch. A model combining these two very popular and practical phenomena is studied. We focus on identical jobs and linear compression cost function. Two versions of the problem are considered: in the first we minimize the sum of the total flowtime and the compression cost, and in the second we minimize the total flowtime subject to an upper bound on the maximum compression. We study both problems on a single machine and on parallel identical machines. In all cases we introduce closed form solutions for the relaxed version (allowing non‐integer batch sizes). Then, a simple rounding procedure is introduced, tested numerically, and shown to generate extremely close‐to‐optimal integer solutions. For a given number of machines, the total computational effort required by our proposed solution procedure is 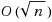$O(\sqrt{n})$ , where 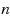$n$ is the number of jobs.