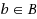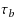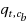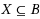The bi‐objective winner determination problem (2WDP‐SC) of a combinatorial procurement auction for transport contracts is characterized by a set B of bundle bids, with each bundle bid
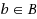 consisting of a bidding carrier c
b
, a bid price p
b
, and a set
consisting of a bidding carrier c
b
, a bid price p
b
, and a set
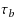 of transport contracts which is a subset of the set T of tendered transport contracts. Additionally, the transport quality
of transport contracts which is a subset of the set T of tendered transport contracts. Additionally, the transport quality
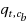 is given which is expected to be realized when a transport contract t is executed by a carrier c
b
. The task of the auctioneer is to find a set X of winning bids (
is given which is expected to be realized when a transport contract t is executed by a carrier c
b
. The task of the auctioneer is to find a set X of winning bids (
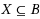 ), such that each transport contract is part of at least one winning bid, the total procurement costs are minimized, and the total transport quality is maximized. This paper presents a metaheuristic approach for the 2WDP‐SC which integrates the greedy randomized adaptive search procedure with a two‐stage candidate component selection procedure, large neighborhood search, and self‐adaptive parameter setting in order to find a competitive set of non‐dominated solutions. The heuristic outperforms all existing approaches. For seven small benchmark instances, the heuristic is the sole approach that finds all Pareto‐optimal solutions. For 28 out of 30 large instances, none of the existing approaches is able to compute a solution that dominates a solution found by the proposed heuristic.
), such that each transport contract is part of at least one winning bid, the total procurement costs are minimized, and the total transport quality is maximized. This paper presents a metaheuristic approach for the 2WDP‐SC which integrates the greedy randomized adaptive search procedure with a two‐stage candidate component selection procedure, large neighborhood search, and self‐adaptive parameter setting in order to find a competitive set of non‐dominated solutions. The heuristic outperforms all existing approaches. For seven small benchmark instances, the heuristic is the sole approach that finds all Pareto‐optimal solutions. For 28 out of 30 large instances, none of the existing approaches is able to compute a solution that dominates a solution found by the proposed heuristic.