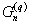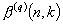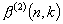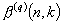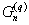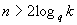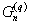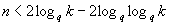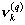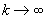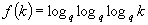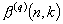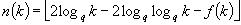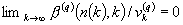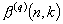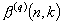The number of cycles of length k that can be generated by q-ary n-stage feedback shift registers is studied. This problem is equivalent to finding the number of cycles of length k in the natural generalization, from binary to q-ary digits, of the so-called de Bruijn-Good graphs. The number of cycles of length k in the q-ary graph 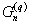 of order n is denoted by
of order n is denoted by 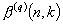 . Known results about
. Known results about 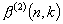 are summarized and extensive new numerical data is presented. Lower and upper bounds on
are summarized and extensive new numerical data is presented. Lower and upper bounds on 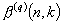 are derived showing that, for large k, virtually all q-ary cycles of length k are contained in
are derived showing that, for large k, virtually all q-ary cycles of length k are contained in 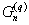 for
for 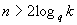 , but virtually none of these cycles is contained in
, but virtually none of these cycles is contained in 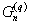 for
for 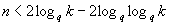 . More precisely, if
. More precisely, if 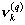 denotes the total number of q-ary lenth-k cycles, then for any function f(k) that grows without bounds as
denotes the total number of q-ary lenth-k cycles, then for any function f(k) that grows without bounds as 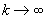 (e.g.
(e.g. 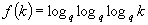 ), the bounds obtained on
), the bounds obtained on 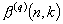 are asymptotically tight in the sense that they imply
are asymptotically tight in the sense that they imply  for
for 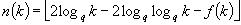 , and
, and 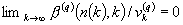 for
for  , where
, where  denotes the integer part of the enclosed number. Finally, some approximations for
denotes the integer part of the enclosed number. Finally, some approximations for 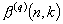 are given that make the global behaviour of
are given that make the global behaviour of 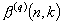 more transparent.
more transparent.